如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,
(1)△ABC与△DBC的面积相等吗?为什么?
(2)若S△AOB=21cm2,求S△COD;
(3)若S△AOD=10cm2,且BO:OD=2:1,求S△ABD.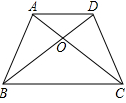
(1)根据已知得出∴△ABC的边BC上的高和△DBC边BC上的高相等,设此高为h,根据三角形的面积公式求出即可;
(2)根据△ABC的面积和△DBC的面积相等,都减去△OBC的面积,即可得出△AOB的面积和△DOC的面积相等;
(3)求出BD=3OD,根据面积公式代入求出即可.
解:(1))△ABC与△DBC的面积相等,理由是:
∵AD∥BC,
∴△ABC的边BC上的高和△DBC边BC上的高相等,设此高为h,
∴△ABC的面积是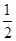 BC×h,△DBC的面积是
BC×h,△DBC的面积是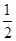 ×BC×h,
×BC×h,
∵BC=BC,
∴△ABC与△DBC的面积相等;
(2)∵S△ABC=S△DBC,
∴S△ABC﹣S△OBC=S△DBC﹣S△OBC,
∴S△AOB=S△DOC=21cm2,
即S△COD=21cm2;
(3)∵BO:OD=2:1,
∴BD=3OD,
∵△AOD的边OD上的高和△ABD的边BD上的高相等,设此高为a,
∵S△AOD=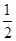 ×OD×a=10cm2,
×OD×a=10cm2,
∴S△ABD.=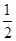 ×BD×a=
×BD×a=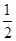 ×3OD×a=3×10cm2=30cm2.
×3OD×a=3×10cm2=30cm2.
【题目】
如图,AF是△ABC的高,AD是△ABC的角平分线,且∠B=38°,∠C=72°,求∠DAF的度数.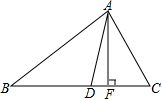
(10 分)我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120 人,乙团队人数不超过50 人.设甲团队人数为x 人,如果甲、乙两团队分别购买门票,两团队门票款之和为W 元.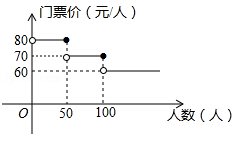
(1)求W 关于x 的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100 人,请说明甲、乙两团队联合购票比分别购票最多可节约多少钱;
(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50 人时,门票价格不变;人数超过50 人但不超过100 人时,每张门票降价a 元;人数超过100 人时,每张门票降价2a 元.在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,最多可节约3400 元,求a 的值.
(8 分)如图,反比例函数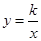 的图象经过点A(
的图象经过点A(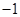 ,4),直线
,4),直线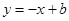 (
( )与双曲线
)与双曲线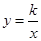 在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.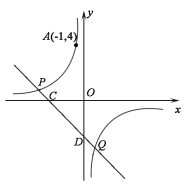
(1)求k 的值;
(2)当 时,求△OCD 的面积;
时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得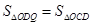 ? 若存在,请求出b 的值;若不存在,请说明理由.
? 若存在,请求出b 的值;若不存在,请说明理由.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O 交AB 于点M,交BC 于点N,连接AN,过点C 的切线交AB 的延长线于点P.
(1)求证:∠BCP=∠BAN;
(2)求证: .
.
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000 米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方.求拦截点D 处到公路的距离(结果不取近似值).
(7 分)“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.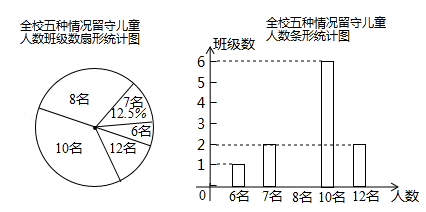
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.