选做题(本小题满分10分)已知集合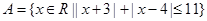 ,
, ,求集合
,求集合 .
.
(本小题满分14分)已知函数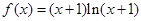 ,
, (
( 为常数,
为常数, 是自然对数的底数),
是自然对数的底数), 为
为 的导函数,且
的导函数,且 ,
,
(1)求 的值;
的值;
(2)对任意 证明:
证明: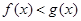 ;
;
(3)若对所有的 ≥0,都有
≥0,都有 ≥ax成立,求实数a的取值范围.
≥ax成立,求实数a的取值范围.
(本小题满分13分)已知定点 ,
,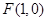 ,定直线
,定直线 :
: ,动点
,动点 与点
与点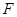 的距离是它到直线
的距离是它到直线 的距离的
的距离的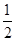 .设点
.设点 的轨迹为
的轨迹为 ,过点
,过点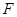 的直线交
的直线交 于
于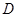 、
、 两点,直线
两点,直线 、
、 与直线
与直线 分别相交于
分别相交于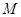 、
、 两点。
两点。
(1)求 的方程;
的方程;
(2)试判断以线段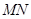 为直径的圆是否过点
为直径的圆是否过点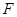 ,并说明理由.
,并说明理由.
(本小题满分12分)已知数列 为等差数列,其中
为等差数列,其中
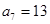 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列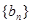 满足
满足 ,
,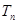 为数列
为数列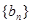 的前
的前 项和,当不等式
项和,当不等式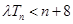 (
(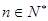 )恒成立时,求实数
)恒成立时,求实数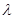 的取值范围.
的取值范围.
(本小题满分12分)如图,四边形ABCD为梯形,AB∥CD, 平面ABCD,
平面ABCD, ,
,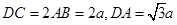 ,E为BC中点.
,E为BC中点.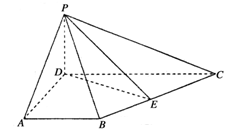
(1)求证:平面 平面PDE;
平面PDE;
(2)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
(本小题满分12分)某学校有男老师45名,女老师15名,按照分层抽样的方法组建了一个4人的学科攻关小组。
(1)求某老师被抽到的概率及学科攻关小组中男、女老师的人数;
(2)经过一个月的学习、讨论,这个学科攻关小组决定选出2名老师做某项实验,方法是先从小组里选出1名老师做实验,该老师做完后,再从小组内剩下的老师中选1名做实验,求选出的2名老师中恰有1名女老师的概率.