如图,直线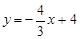 与
与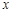 轴交于点
轴交于点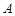 ,与
,与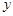 轴交于点
轴交于点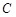 ,已知二次函数的图象经过点
,已知二次函数的图象经过点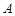 、
、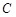 和点
和点 .
.

(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为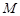 ,求四边形
,求四边形 的面积;
的面积;
(3)有两动点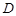 、
、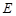 同时从点
同时从点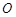 出发,其中点
出发,其中点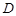 以每秒
以每秒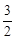 个单位长度的速度沿折线
个单位长度的速度沿折线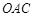 按
按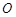 →
→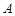 →
→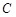 的路线运动,点
的路线运动,点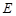 以每秒
以每秒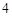 个单位长度的速度沿折线
个单位长度的速度沿折线 按
按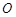 →
→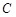 →
→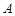 的路线运动,当
的路线运动,当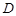 、
、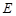 两点相遇时,它们都停止运动.设
两点相遇时,它们都停止运动.设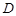 、
、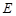 同时从点
同时从点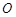 出发
出发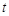 秒时,
秒时,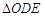 的面积为S .
的面积为S .
①请问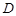 、
、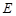 两点在运动过程中,是否存在
两点在运动过程中,是否存在 ∥
∥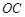 ,若存在,请求出此时
,若存在,请求出此时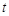 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②请求出S关于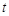 的函数关系式,并写出自变量
的函数关系式,并写出自变量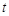 的取值范围;
的取值范围;
③设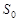 是②中函数S的最大值,那么
是②中函数S的最大值,那么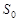 = .
= .
某车间生产螺钉和螺母,每人每天平均生产1200个螺钉或2000个螺母。为了使每天的产品刚好是一个螺钉与两个螺母配套,请你给22名工人安排一下分工。
按照上北下南,左西右东的规定画出表示东南西北的十字线,然后在图上画出表示下列方向的射线:北偏西30o
南偏东60o
北偏东15o
西南方向
如图,一次函数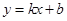 的图像与反比例函数
的图像与反比例函数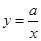 的图像交于
的图像交于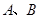 两点,与
两点,与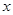 轴交于点
轴交于点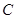 ,与
,与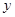 轴交于点
轴交于点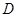 ,已知
,已知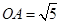 ,点
,点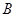 的坐标为
的坐标为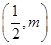 ,过点
,过点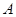 作
作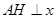 轴,垂足为
轴,垂足为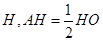
求反比例函数和一次函数的解析式
求
 的面积
的面积
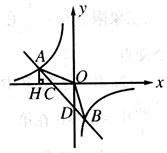
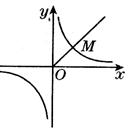
如图所示,在平面直角坐标系中,第一象限的角平分线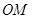 与反比例函数的图像相交于点
与反比例函数的图像相交于点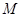 ,已知
,已知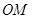 的长是
的长是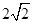 。
。
求点
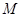 的坐标;
的坐标;求此反比例函数的关系式
已知直线y = x+m与x轴、y轴分别交于点A、B,与双曲线y
= x+m与x轴、y轴分别交于点A、B,与双曲线y =
=  分别交于点C、D,且点C的坐标为(-1,2).
分别交于点C、D,且点C的坐标为(-1,2).分别求出直线AB及双曲线的函数表达式;
利用图像直接写出:当x在什么范围内取值时y
 >y
>y