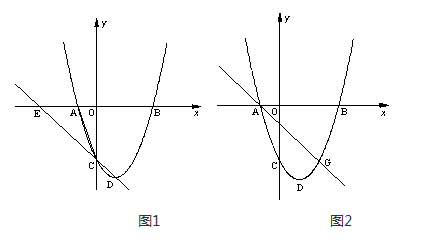
如图1,在平面直角坐标系中,二次函数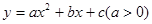 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=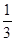 .
.
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(本小题满分5分)
已知二次函数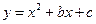 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:
 |
… |
 |
 |
 |
 |
 |
 |
… |
 |
… |
 |
 |
 |
 |
 |
 |
… |
(1)求该二次函数的关系式;
(2)当 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若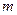 ≥2,且
≥2,且 ,
,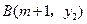 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较 与
与 的大小.
的大小.
(本小题满分5分)
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)要使该二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移多少个单位?
(本小题满分5分)
如图,在梯形 中,
中,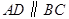 ,
,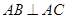 ,
,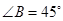 ,
,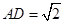 ,
,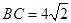 ,求
,求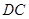 的长.
的长.
(本小题满分5分)
如图,梯形ABCD中,AB∥CD,F是DC的中点,BF的延长线交射线AD于点G,, BG 交AC于点E.求证:=.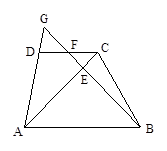
(本小题满分5分)
如图,在△ACD中,B为AC上一点,且 ,
,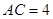 ,
,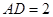 ,求AB的长.
,求AB的长.