已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
如图,(1)至(10)个图案中都是对称图形,请观察并指出哪些是轴对称图形,哪些图案成轴对称.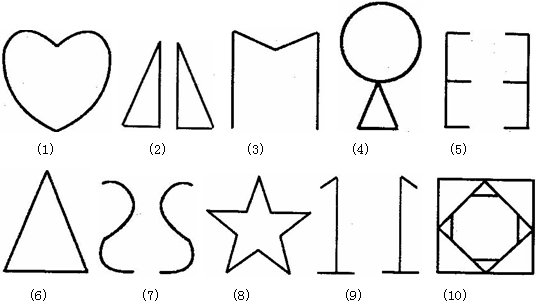
某辆汽车行驶路程与时间的关系如图所示,描述这辆汽车的行驶情况,并分别计算前3h内,前5h内和全程的平均速度,描述这辆汽车的行驶情况,这辆汽车共行驶多长时间?多少路程?
小欣外出办事,先以12km/h速度骑自行车前进半小时,再乘公共汽车以40km/h速度行驶20min,接着以6km/h速度步行30min,休息10min后,又以5km/h速度步行20min,到达目的地,在这个过程中,哪个是自变量哪个是因变量,画出表示自变量与因变量关系的图像.
如图,是李老师骑自行车上班途中,骑车路程与时间的关系,根据图像合理想像李老师上班途中的情况.
汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,下面的图像表示了一辆汽车在山区行驶过程中的速度随时间变化的情况.
(1)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(2)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上花时间最长?
(3)用自己的语言大致描述这辆汽车的行驶情况,包括遇到的山路,在山路上的速度变化情况等.