(本小题满分12分)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
| |
常喝 |
不常喝 |
合计 |
| 肥胖 |
|
2 |
|
| 不肥胖 |
|
18 |
|
| 合计 |
|
|
30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为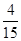 .
.
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(Ⅲ)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?参考数据:
(本小题满分7分)
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作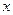 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作 ,令
,令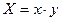 。
。
(Ⅰ)求 所取各值的概率;
所取各值的概率;
(Ⅱ)求 的分布列,并求出
的分布列,并求出 的数学期望值。
的数学期望值。
(本小题满分8分)
已知直线的极坐标方程为 ,圆
,圆 的参数方程
的参数方程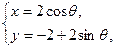 (其中
(其中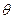 为参数)。
为参数)。
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)将圆的参数方程化为普通方程;
(Ⅲ)求圆 上的点到直线的距离的最小值。
上的点到直线的距离的最小值。
已知圆(x-1)2+(y-1)2=1和点A(2a,0),B(0,2b)且a>1, b>1.
(1)若圆与直线A B相切,求a和b之间的关系式;
B相切,求a和b之间的关系式;
(2)若圆与直线AB相切且△AOB面积最小,求直线AB的方程.(O为坐标原点)
如图,在直三棱柱 中,
中, ,
, ,
, 为的
为的 中点.(1)求证:
中点.(1)求证: ⊥平面
⊥平面 ;(2)设
;(2)设 是
是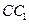 上一点,试确定
上一点,试确定 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 ,并说明理由.
,并说明理由.
已知 的顶点A为(3,-1),AB边上的中线所在直线方程为
的顶点A为(3,-1),AB边上的中线所在直线方程为 ,
,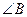 的平分线所在直线方程为
的平分线所在直线方程为 ,求BC边所在直线的方程.
,求BC边所在直线的方程.