（本小题满分16分）设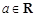
，函数
．
（1）若
为奇函数，求
的值；
（2）若对任意的
，
恒成立，求的取值范围；
（3）当
时，求函数
零点的个数．
设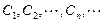
是坐标平面上的一列圆，它们的圆心都在
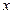轴的正半轴上，且都与直线
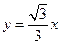相切，对每一个正整数
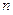,圆
都与圆
相互外切，以
表示的半径，已知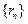
为递增数列.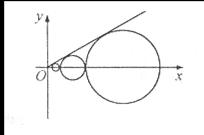
(Ⅰ)证明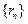：为等比数列；
（Ⅱ）设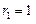
，求数列
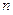的前项和.
已知三棱锥P－ABC中，PA⊥面ABC，AB⊥AC，PA=AC=½AB，N为AB上一点，AB=4AN,M,S分别为PB,BC的中点.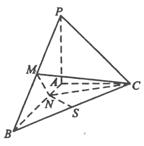
（Ⅰ）证明：CM⊥SN；
（Ⅱ）求SN与平面CMN所成角的大小。
已知动圆M与圆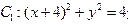
外切，圆
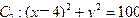内切
求动圆圆心M 的轨迹方程。
已知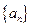
为等差数列，且
，
。
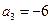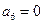（Ⅰ）求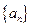的通项公式；
（Ⅱ）若等比数列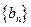
满足
，
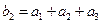，求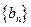的前n项和公式。
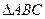的面积是30，内角
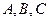所对边长分别为
，
。
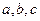(Ⅰ)求
；
(Ⅱ)若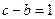
，求
的值。