(本小题满分14分)如图,已知 中,
中, ,
, ,
, ⊥
⊥
平面 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)设平面
 平面
平面 ,求证
,求证 ;
;
(3)求四棱锥B-CDFE的体积V.
(本小题满分14分)已知椭圆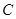 :
: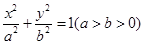 的上顶点为
的上顶点为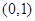 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆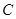 的方程;
的方程;
(Ⅱ)证明:过椭圆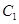 :
: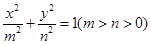 上一点
上一点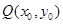 的切线方程为
的切线方程为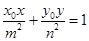 ;
;
(Ⅲ)从圆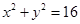 上一点
上一点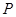 向椭圆
向椭圆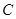 引两条切线,切点分别为
引两条切线,切点分别为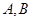 ,当直线
,当直线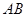 分别与
分别与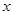 轴、
轴、 轴交于
轴交于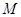 、
、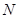 两点时,求
两点时,求 的最小值.
的最小值.
(本小题满分13分)某校A,B两个班级各有5名编号为1,2,3,4,5的学生进行射击训练,每人射击10次,击中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| A班 |
9 |
7 |
8 |
6 |
5 |
| B班 |
7 |
8 |
9 |
7 |
4 |
(Ⅰ)从统计数据看,A,B两个班哪个班成绩更稳定(用数据说明)?
(Ⅱ)在本次训练中,从两班中分别任选一个同学,比较两人的击中次数,求A班同学击中次数低于B班同学击中次数的概率.
(本小题满分14分)已知椭圆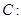
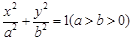 的右焦点为
的右焦点为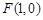 ,且点
,且点 在椭圆
在椭圆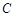 上,
上, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆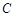 的标准方程;
的标准方程;
(Ⅱ)设过定点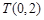 的直线
的直线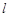 与椭圆
与椭圆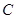 交于不同的两点
交于不同的两点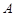 、
、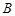 ,且
,且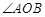 为锐角,求直线
为锐角,求直线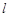 的斜率
的斜率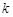 的取值范围;
的取值范围;
(Ⅲ)过椭圆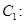
 上异于其顶点的任一点
上异于其顶点的任一点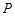 ,作圆
,作圆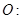
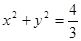 的两条切线,切点分别为
的两条切线,切点分别为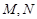 (
(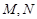 不在坐标轴上),若直线
不在坐标轴上),若直线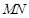 在
在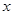 轴、
轴、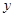 轴上的截距分别为
轴上的截距分别为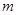 、
、 ,证明:
,证明: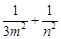 为定值.
为定值.
(本小题满分13分)已知实数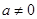 ,函数
,函数 .
.
(1)当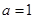 时,讨论函数
时,讨论函数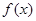 的单调性;
的单调性;
(2)若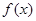 在区间
在区间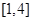 上是增函数,求实数
上是增函数,求实数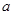 的取值范围;
的取值范围;
(3)若当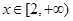 时,函数
时,函数 图象上的点均在不等式
图象上的点均在不等式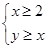 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数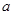 的取值范围.
的取值范围.
(本小题满分12分)已知数列 是等比数列,首项
是等比数列,首项 ,公比
,公比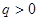 ,其前
,其前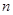 项和为
项和为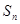 ,且
,且 ,
,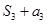 ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列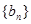 满足
满足 ,
,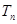 为数列
为数列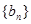 的前
的前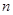 项和,若
项和,若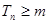 恒成立,求
恒成立,求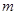 的最大值.
的最大值.