如图,在平面直角坐标系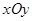 中,椭圆
中,椭圆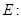
 的左顶点为
的左顶点为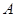 ,与
,与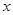 轴平行的直线与椭圆
轴平行的直线与椭圆 交于
交于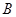 、
、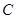 两点,过
两点,过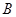 、
、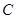 两点且分别与直线
两点且分别与直线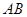 、
、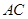 垂直的直线相交于点
垂直的直线相交于点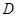 .已知椭圆
.已知椭圆 的离心率为
的离心率为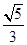 ,右焦点到右准线的距离为
,右焦点到右准线的距离为 .
. 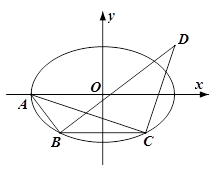
(1)求椭圆 的标准方程;
的标准方程;
(2)证明点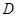 在一条定直线上运动,并求出该直线的方程;
在一条定直线上运动,并求出该直线的方程;
(3)求 面积的最大值.
面积的最大值.
【2015高考新课标1,文23】选修4-4:坐标系与参数方程
在直角坐标系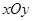 中,直线
中,直线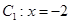 ,圆
,圆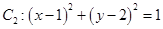 ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(Ⅰ)求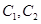 的极坐标方程.
的极坐标方程.
(Ⅱ)若直线 的极坐标方程为
的极坐标方程为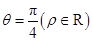 ,设
,设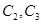 的交点为
的交点为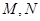 ,求
,求 的面积.
的面积.
【2015高考新课标1,文22】选修4-1:几何证明选讲
如图AB是 O直径,AC是
O直径,AC是 O切线,BC交
O切线,BC交 O与点E.
O与点E.
(Ⅰ)若D为AC中点,求证:DE是 O切线;
O切线;
(Ⅱ)若 ,求
,求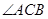 的大小.
的大小.
【2015高考陕西,文24】选修4-5:不等式选讲
已知关于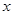 的不等式
的不等式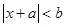 的解集为
的解集为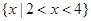
(Ⅰ)求实数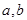 的值;
的值;
(Ⅱ)求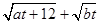 的最大值.
的最大值.
【2015高考陕西,文23】选修4-4:坐标系与参数方程
在直角坐标版权法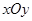 吕,直线
吕,直线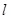 的参数方程为
的参数方程为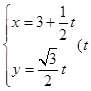 为参数),以原点为极点,
为参数),以原点为极点,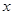 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系,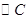 的极坐标方程为
的极坐标方程为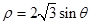 .
.
(Ⅰ)写出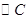 的直角坐标方程;
的直角坐标方程;
(Ⅱ)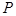 为直线
为直线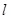 上一动点,当
上一动点,当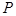 到圆心
到圆心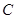 的距离最小时,求点
的距离最小时,求点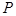 的坐标.
的坐标.
【2015高考陕西,文22】选修4-1:几何证明选讲
如图,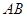 切
切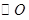 于点
于点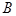 ,直线
,直线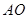 交
交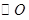 于
于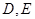 两点,
两点,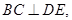 垂足为
垂足为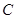 .
.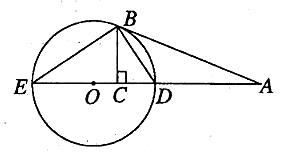
(Ⅰ)证明: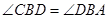
(Ⅱ)若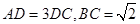 ,求
,求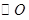 的直径.
的直径.