命题：若a＞b，则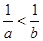
．
（1）请判断这个命题的真假．若是真命题请证明；若是假命题，请举一个反例；
（2）请你适当修改命题的题设使其成为一个真命题．
（本题10分）化简求值：5(3a2b－ab2) －(ab2+3a2b), 其中a=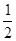
，b=
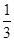
解方程（每小题2分，共12分）
（1）
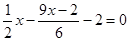；（2）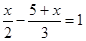
（本题8分）把下列各数在数轴上表示出来，并按从小到大的顺序用“＜”连接起来．
-3．5， 0， 2， -2 , 0．5．
如图，在平面直角坐标系中，以点M（0，3）为圆心、5为半径的圆与x轴交于点A、B（点A在点B的左侧），与y轴交于点C、D（点C在点D的上方），经过B、C两点的抛物线的顶点E在第二象限．
（1）求点A、B两点的坐标．
（2）当抛物线的对称轴与⊙M相切时, 求此时抛物线的解析式．
（3）连结AE、AC、CE，若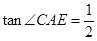
．①求点E坐标；②在直线BC上是否存在点P，使得以点B、M、
P为顶点的三角形和△ACE相似？若存在，直接写出点P的坐标；若不存在，请说明理由．
国家推行“节能减排\低碳经济”政策后，低排量的汽车比较畅销，某汽车经销商购进A，B两种型号的低排量汽车，其中A型汽车的进货单价比B型汽车的进货单价多2万元,花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相等，销售中发现A型汽车的每周销量
（台）与售价
（万元/台）满足函数关系式
，B型汽车的每周销量
（台）与售价万元/台）满足函数关系式
．
（1）求A、B两种型号的汽车的进货单价；
（2）已知A型汽车的售价比B型汽车的人售价高2万元/台，设B型汽车售价为
万元/台．每周销售这两种车的总利润为
万元，求与的函数关系式，A、B两种型号的汽车售价各为多少时，每周销售这两种车的总利润最大？最大总利润是多少万元？