已知△ABC的三边分别为x、y、z.
(1)以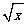 、
、 、
、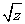 为三边的三角形一定存在;
为三边的三角形一定存在;
(2)以x2、y2、z2为三边的三角形一定存在;
(3)以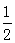 (x+y)、
(x+y)、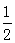 (y+z)、
(y+z)、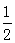 (z+x)为三边的三角形一定存在;
(z+x)为三边的三角形一定存在;
(4)以|x﹣y|+l、|y﹣z|+l、|z﹣x|+l为三边的三角形一定存在.
以上四个结论中,正确结论的个数为( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
在一次九年级学生视力检查中.随机检查了8个人的右眼视力,结果如下:4.0,4.2,4.5,4.0,4.4,4.5,4.0,4.8.则下列说法中正确的是( )
| A.这组数据的中位数是4.4 | B.这组数据的众数是4.5 |
| C.这组数据的平均数是4.3 | D.这组数据的极差是0.5 |
如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
| A.2cm | B.3cm |
| C.4cm | D.2 cm cm |
化简(x﹣ )÷(1﹣
)÷(1﹣ )的结果是( )
)的结果是( )
A. |
B.x﹣1 |
C. |
D. |
计算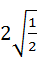 ﹣6
﹣6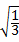 +
+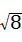 的结果是( )
的结果是( )
A.3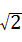 ﹣2 ﹣2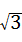 |
B.5﹣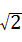 |
C.5﹣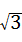 |
D.2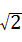 |
如图.己知AB∥CD,∠1=70°,则∠2的度数是( )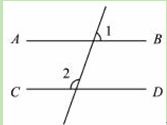
| A.60° | B.70° |
| C.80° | D.110 |