如图,梯形ABCD中,AD∥BC,∠BAD=90°,AD=1,E为AB的中点,AC是ED的垂直平分线.
(1)求证:DB=DC;
(2)在图(2)的线段AB上找出一点P,使PC+PD的值最小,标出点P的位置,保留画图痕迹,并求出PB的值.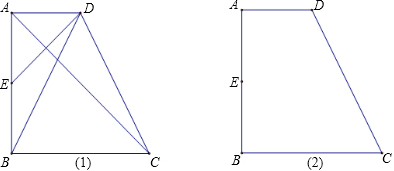
(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证: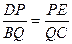 .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.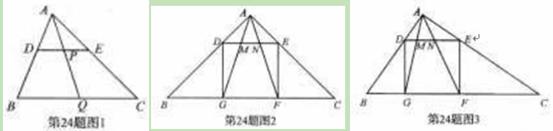
星光中学课外活动小组准备围建一个矩形生物苗圃园.其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关系式及其自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值;
(3)当这个苗圃园的面积不小于88平方米时,试结合函数图像,直接写出x的取值范围.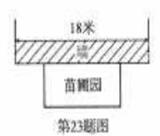
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
(1)求证:PB为⊙O的切线;
(2)若tan∠ABE= ,求sinE的值.
,求sinE的值.
在平面直角坐标系中,△ABC的顶点坐标是A(-7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,-1),E(-1,-7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.