已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为______;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.
在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m; =1.44,
=1.44,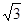 =1.732,
=1.732, =2.236,以上数据供参考)
=2.236,以上数据供参考)
小明要在半径为1m,圆心角为60°的扇形铁皮上剪取一块面积尽可能大的正方形铁皮.小明在扇形铁皮上设计了如图所示的甲、乙两种方案剪取所得的正方形的面积,并计算哪个正方形的面积较大?(估算时 取1.73,结果保留两个有效数字)
取1.73,结果保留两个有效数字)
如图,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC,求:
(1)被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆半径是多少?(结果可用根号表示)
如图,粮仓的顶部是圆锥形,这个圆锥的底面周长为36m,母线长为8m,为防雨需在粮仓顶部铺上油毡,如果按用料的10%计接头重合部分,那么这座粮仓实际需用油毡的面积是多少?
用一块圆心角为300°的扇形铁皮做一个圆锥形烟囱帽,圆锥的底面直径为1m,求这个扇形铁皮的半径.