如图,△ABC中A(﹣4,4),B(﹣8,0),O(0,0).
(1)△ABC沿x轴向右平移8个单位得到△DOE,则点A的对应点D的坐标为________
(2)△ABC绕O点顺时针旋转135°得到△FGO,作出△DOE和△FGO,并求出它们重叠部分图形的周长.
如图,一次函数y=kx+1(k≠0)与反比例函数y=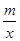 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
如图,依据闯关游戏规则,请你探究“闯关游戏”的奥秘:
(1)用列表的方法表示有可能的闯关情况;
(2)求出闯关成功的概率.
解一元二次方程:3(x﹣2)2=x(x﹣2).
计算:6cos45°-|4- |+
|+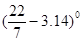 +(-
+(-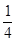 )-1
)-1
如图1,已知抛物线y=-x2+bx+c经过点A(1,0),B(-3,0)两点,且与y轴交于点C.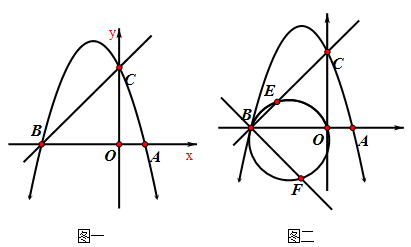
(1)求b,c的值.
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值. 若不存在,请说明理由.
(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.