在平面直角坐标系中，画出三角形ABC，使它的三个顶点坐标分别是A（4，3），B（3，1），C（1，2）．再将三角形ABC三个顶点的横坐标都减去5，纵坐标都减去4，分别得到点A1、B1、C1各点，依次连接A1、B1、C1三点，所得三角形A1B1C1，与三角形ABC的大小、形状和位置有什么关系？
已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.
(1)求抛物线的解析式；
(2)求△MCB的面积S△MCB.
已知二次函数
的图象过点（-1，15），
求m的值；
若二次函数图象上有一点C，图象与x轴交于A、B两点，且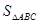
=3，求点C的坐标。
如图，水库大坝的横断面是梯形，坝顶宽BC=10米，坝高BE=CF=30米，斜坡AB的坡角∠A=30°，斜坡CD的坡度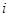
=1:3，求坝底宽AD的长.（结果保留根号）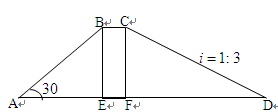
已知函数图象如图所示，根据图象可得：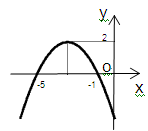
（1）抛物线顶点坐标；
（2）对称轴为；
（3）当x=时，y有最大值是；
（4）当时，y随着x得增大而增大。
（5）当时，y＞0.
已知：在
ABC中，∠B=45°，∠C =60°，BC=8．
求AC的长(结果保留根号).