为了增强居民的节约用电意识，某市拟出台居民阶梯电价政策：每户-优题课

“立定跳远”是我市初中毕业生体育测试项目之一．测试时，记录下学生立定跳远的成绩，然后按照评分标准转化为相应的分数，满分10分．其中男生立定跳远的评分标准如下：注：成绩栏里的每个范围，含最低值，不含最高值．

成绩（米）	…	1.80～1.86	1.86～1.94	1.94～2.02	2.02～2.18	2.18～2.34	2.34～
得分	…	5	6	7	8	9	10

某校九年级有480名男生参加立定跳远测试，现从中随机抽取10名男生测试成绩（单位：分）如下：
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题：
（1）求这10名男生立定跳远成绩的极差和平均数；
（2）求这10名男生立定跳远得分的中位数和众数；
（3）如果将9分（含9分）以上定为“优秀”，请你估计这480名男生中得优秀的人数．

我国是一个严重缺水的国家，为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过6吨时，水价为每吨2元，超过6吨时，超过的部分按每吨3元收费，该市某户居民5月份用水x吨，应交水费y元．
（1）请写出y与x的函数关系式．
（2）如果该户居民这个月交水费27元，那么这个月该户用了多少吨水？

先化简，再求值：,其中，．

张先生准备在沙坪坝购买一套小户型商品房，他去某楼盘了解情况得知, 该户型商品房的单价是8000元/，面积如图所示（单位：米，卫生间的宽未定，设宽为米），售房部为张先生提供了以下两种优惠方案：
方案一：整套房的单价是8000元/，其中厨房可免费赠送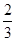的面积；
方案二：整套房按原销售总金额的9折出售．
（1）用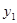表示方案一中购买一套该户型商品房的总金额，用表示方案二中购买一套该户型商品房的总金额，分别求出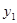、与的关系式；
（2）求取何值时，两种优惠方案的总金额一样多？
（3）张先生因现金不够，于2012年1月在建行借了9万元住房贷款，贷款期限为6年，从开始贷款的下一个月起逐月偿还，贷款月利率是0.5%，每月还款数额=平均每月应还的贷款本金数额+月利息，月利息=上月所剩贷款本金数额×月利率．
①张先生借款后第一个月应还款数额是多少元？
②假设贷款月利率不变，若张先生在借款后第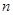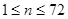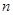（，是正整数）个月的还款数额为P，请写出P与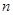之间的关系式．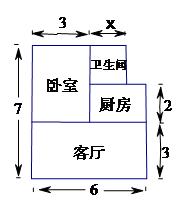

某公司要把240吨白砂糖运往某市的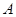、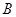两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往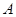地的运费为：大车630元/辆，小车420元/辆；运往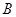地的运费为：大车750元/辆，小车550元/辆.
（1）求两种货车各用多少辆；
（2）如果安排10辆货车前往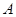地，其中调往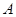地的大车有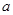辆，其余货车前往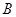地，若设总运费为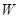，求W与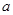的关系式（用含有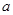的代数式表示W）.

	4月份总用电量/千瓦时	电费/元
小刚	200
小丽	300