如图,在平面直角坐标系中,点A、B分别在x轴y轴的正半轴上,线段OA的长是不等式5x﹣4<3(x+2)的最大整数解,线段OB的长是一元二次方程x2﹣2x﹣3=0的一个根,将Rt△ABO沿BE折叠,使AB边落在OB边所在的y轴上,点A与点D重合.
(1)求OA、OB的长;
(2)求直线BE的解析式;
(3)在平面内是否存在点M,使B、O、E、M为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.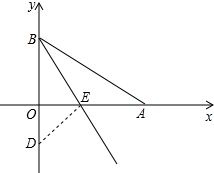
温州移动公司推出两种通讯业务:(1)“全球通”:用户先交50元月租费,然后每通话一分钟,付话费0.4元(市内通话);(2)“金卡神州行”,用户不交月租费,每通话一分钟,付话费0.6元(市内通话)。
(1)按一个月通话x分钟计算,请你分别写出两种收费方式下,客户应支付的费用(用含有x的代数式表示);
(2)求当一个月通话多少分钟时,两种收费方式支付的费用相同;
(3)某用户一个月内通话时间大约为200分钟,你认为选择哪种通讯业务较合适并说明理由?
先化简,再求值: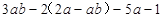 ,其中
,其中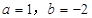
解下列方程
(1)2(x-3)=x;
(2)x- -1.
-1.
计算:
(1)-1+4-2
(2)―12×(1 ―
―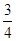 +
+ )
)
(3)
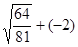
(4)
把下列各数在数轴上表示出来,并用“<”号把这些数连接起来.  ,
, ,-3,
,-3, 。
。