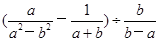(本题7分)某自行车厂一周计划生产2100辆电动车,平均每天生产电动车300辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的生产情况(超产记为正、减产记为负,单位:辆):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 减增 |
+8 |
-2 |
-6 |
+11 |
-12 |
+6 |
+7 |
(1)根据记录的数据可知,该厂星期一生产电动车 辆
(2)产量最多的一天比产量最少的一天多生产电动车 辆
(3)该厂实行记件工资制,每生产一辆车可得60元,若超额完成任务,则超额部分每辆车另奖10元,每少生产一辆扣10元,那么该厂工人这一周的工资总额是多少元?
如图,C是以AB为直径的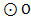 上一点,过点O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
上一点,过点O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
(1)求证:PC是⊙O的切线;
(2)若AF=1,OA=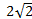 , 求PC的长。
, 求PC的长。
城市规划期间,欲拆除一电线杆AB(如图所示),已知距电线杆AB水平距离14米的D处有一大坝,背水坡CD的坡度i=2:1,坝高CF为2米,在坝顶C处测得杆顶A的仰角为30°,D,E之间是宽为2米的人行道。(
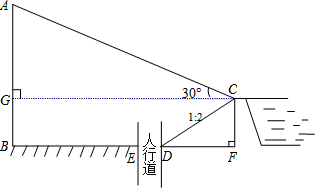
(1)求BF的长度;
(2)在拆除电线杆AB时,为确保行人安全,是否需将此人行道封上?
某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A,B两种产品共50件,已知生产1件A种产品需甲种原料9千克,乙种原料3千克,可获利700元;生产1件B种产品需甲种原料4千克,乙种原料10千克,可获利1200元,设工厂生产A,B两种产品可获总利润是y元,其中甲种产品的生产件数是x,
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值。
有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片片它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q)
(1)请用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数根的概率。
(1)计算: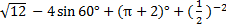 ;
;
(2)化简: