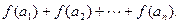如图,在平面直角坐标系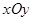 中,点
中,点 ,直线
,直线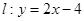 .设圆
.设圆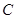 的半径为
的半径为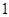 ,圆心在
,圆心在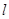 上.
上.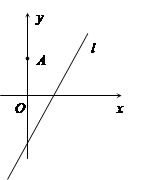
(1)若圆心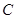 也在直线
也在直线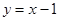 上,过点
上,过点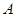 作圆
作圆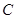 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆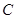 上存在点
上存在点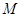 ,使
,使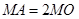 ,求圆心
,求圆心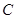 的横坐标
的横坐标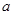 的取值范围.
的取值范围.
(本小题满分12分)
已知等差数列 的首项
的首项 公差
公差 且第二项、第五项、第十四项分别是等比数列
且第二项、第五项、第十四项分别是等比数列 的第二项、第三项、第四项。
的第二项、第三项、第四项。
(1)求数列 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数 均有
均有 成立,
成立,
(3)求数列 的前
的前 项和
项和
(本小题满分12分)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作。比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。
假设每个运动员完成每个系列中的K和D两个动作的得分是相互独立的。根据赛前训练的统计数据,某运动员完成甲系列和乙系列中的K和D两个动作的情况如下表:
表1:甲系列表2:乙系列
| 动作 |
K动作 |
D动作 |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
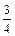 |
 |
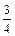 |
 |
| 动作 |
K动作 |
D动作 |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
 |
 |
 |
现该运动员最后一个出场,之前其他运动员的最高得分为115分。
(1)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由。
并求其获得第一名的概率。
(2)若该运动员选择乙系列,求其成绩 的分布列及数学期望
的分布列及数学期望
(本小题满分12分)
已知函数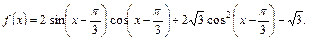
(1)求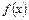 的单调递增区间;
的单调递增区间;
(2)求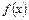 的最大值及取得最大值时相应的
的最大值及取得最大值时相应的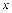 的值。
的值。
(本小题满分12分)
已知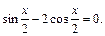
(1)求 的值;
的值;
(2)求 的值。
的值。
已知函数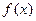 的定义域为[0,1]且同时满足:①对任意
的定义域为[0,1]且同时满足:①对任意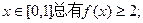 ②
②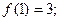 ③若
③若
(I)求 的值;
的值;
(II)求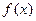 的最大值;
的最大值;
(III)设数列 的前n项和为Sn,且
的前n项和为Sn,且 ,
,
求: