如图,△ABC中,AB=AC,以AC为直径的⊙O与边BC交于点E.过E作直线与AB垂直,垂足为F,且与AC的延长线交于点G.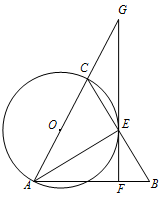
(1)判断直线FG与⊙O的位置关系,并证明你的结论;
(2)若BF=1,CG=2,求⊙O半径.
已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.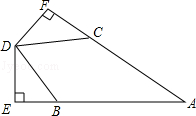
如图所示,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.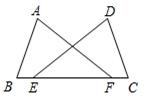
作图题:下图是单位长度为1的正方形网格.
(1)在图1中画出一条以格点为端点,长度为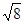 的线段AB;
的线段AB;
(2)在图2中画出一个以格点为顶点,面积为10的正方形ABCD.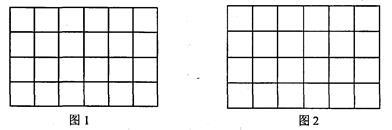
计算题(每题4分,共8分)
(1)9x2-100=0
(2)(x+l)3=8
同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:
(1)求|5-(-2)|=
(2)同样道理|x+5|+|x-2|表示数轴上有理数x所对点到-5和2所对的两点距离之和,请你找出所有符合条件的整数x,使得|x+5|+|x-2|=7,这样的整数是 .
(3)由以上探索猜想对于任何有理数x,|x-3|+|x-6|是否有最小值?如果有,写出最小值;如果没有,说明理由.