已知抛物线y=ax2+bx+c经过A（3，0）、B（0，3）、C（1，0）三点．
（1）求抛物线的解析式；
（2）若点D的坐标为（﹣1，0），在直线AB上有一点P，使△ABO与△ADP相似，求出点P的坐标；
（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．
解不等式组
，并把解集在数轴上表示.
先化简,再求值
其
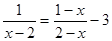
如图，Rt△AOC中，∠ACO=90°，∠AOC=30°．将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO，BO、CO恰好分别在y轴、x轴上．再将Rt△BCO沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．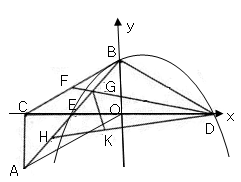
填空：CE:ED=________,AB:AC=__________；
若BH=
，求直线BD解析式在（2）的条件下，一抛物线过点D、点E、点B，此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值？若有，请求出点Q的坐标；若无，请说明理由
如图，AB、ED是⊙O的直径，点C在ED延长线上, 且∠CBD =∠FAB．点F在⊙O上，且 AB⊥DF．连接AD并延长交BC于点G．
求证：BC是⊙O的切线；
求证：BD·BC=BE·CD；
若⊙O 的半径为r，BC=3r，求tan∠CDG的值