如图,Rt△AOC中,∠ACO=90°,∠AOC=30°.将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO,BO、CO恰好分别在y轴、x轴上.再将Rt△BCO沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.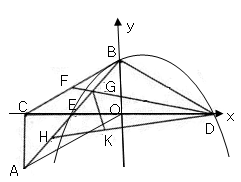
填空:CE:ED=________,AB:AC=__________;
若BH=
 ,求直线BD解析式
,求直线BD解析式在(2)的条件下,一抛物线过点D、点E、点B,此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值?若有,请求出点Q的坐标;若无,请说明理由
【证明体验】
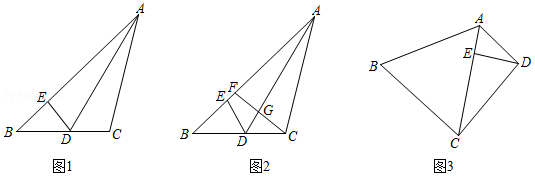
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.
某通讯公司就手机流量套餐推出三种方案,如下表:
|
方案 |
方案 |
方案 |
|
|
每月基本费用(元 |
20 |
56 |
266 |
|
每月免费使用流量(兆 |
1024 |
|
无限 |
|
超出后每兆收费(元 |
|
|
, , 三种方案每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系如图所示.
(1)请写出 , 的值.
(2)在 方案中,当每月使用的流量不少于1024兆时,求每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择 方案最划算?

我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈 能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈 已滑动到点 的位置,且 , , 三点共线, , 为 中点.当 时,伞完全张开.
(1)求 的长.
(2)当伞从完全张开到完全收拢,求伞圈 沿着伞柄向下滑动的距离.
(参考数据: , ,

图1表示的是某书店今年 月的各月营业总额的情况,图2表示的是该书店"党史"类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店 月的营业总额一共是182万元,观察图1、图2,解答下列问题:

(1)求该书店4月份的营业总额,并补全条形统计图.
(2)求5月份"党史"类书籍的营业额.
(3)请你判断这5个月中哪个月"党史"类书籍的营业额最高,并说明理由.
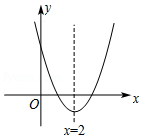
如图,二次函数 为常数)的图象的对称轴为直线 .
(1)求 的值.
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.