某通讯公司就手机流量套餐推出三种方案,如下表:
方案 |
方案 |
方案 |
|
每月基本费用(元 |
20 |
56 |
266 |
每月免费使用流量(兆 |
1024 |
|
无限 |
超出后每兆收费(元 |
|
|
, , 三种方案每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系如图所示.
(1)请写出 , 的值.
(2)在 方案中,当每月使用的流量不少于1024兆时,求每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择 方案最划算?

如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
(1)求证:△AMD≌△BME;
(2)若N是CD的中点,且MN =5,BE=2,求BC的长.
=5,BE=2,求BC的长.
先化简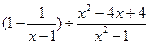 ,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
如图,y关于x的二次函数y=﹣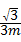 (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.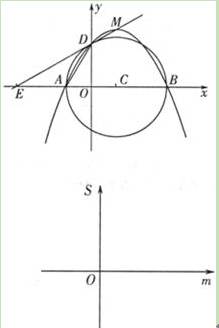
如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.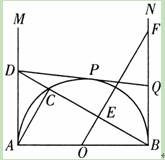
2010年上半年,某种农产品受不良炒作的影响,价格一路上扬.8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份,该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至12月份,月平均价袼y元/千克与月份x呈二次函数关系.已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
(1)分别求出当1≤x≤7和7≤x≤12时,y关于x的函数关系式;
(2)2010年的12个月中.这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?