如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.

(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.
一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有 种可能的结果.
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题: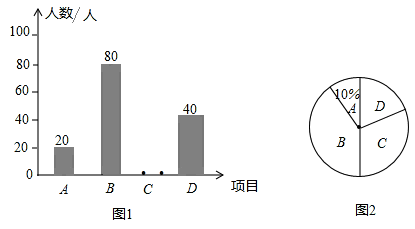
(1)这次被调查的学生共有 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以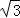 cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
(1)当P异于A.C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?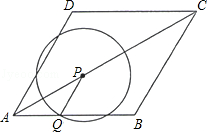
)对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(2)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.试求点M(2,1)到直线y=x+2的直角距离.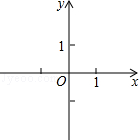
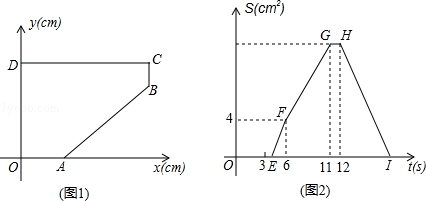
如图1,A.D分别在x轴和y轴上,CD∥x轴,BC∥y轴.点P从D点出发,以1cm/s的速度,沿五边形OABCD的边匀速运动一周.记顺次连接P、O、D三点所围成图形的面积为Scm2,点P运动的时间为ts.已知S与t之间的函数关系如图2中折线段OEFGHI所示.
(1)求A.B两点的坐标;
(2)若直线PD将五边形OABCD分成面积相等的两部分,求直线PD的函数关系式.