如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以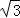 cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
(1)当P异于A.C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?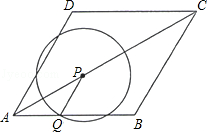
(1)计算: .
(2)化简: .
如图, 是半径为3的 的一条弦, ,点 是 上的一个动点(不与点 , 重合),以 , , 为顶点作 .
(1)如图2,若点 是劣弧 的中点.
①求证: 是菱形;
②求 的面积.
(2)若点 运动到优弧 上,且 有一边与 相切.
①求 的长;
②写出 对角线所夹锐角的正切值.

电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板上人的质量 之间的函数关系式为 (其中 , 为常数, ,其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻 的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为 ,该读数可以换算为人的质量 ,
温馨提示:①导体两端的电压 ,导体的电阻 ,通过导体的电流 ,满足关系式 ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压
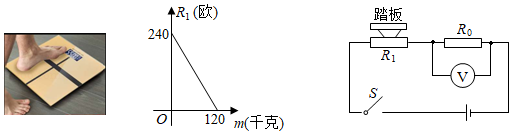
(1)求 , 的值;
(2)求 关于 的函数解析式;
(3)用含 的代数式表示 ;
(4)若电压表量程为 伏,为保护电压表,请确定该电子体重秤可称的最大质量.
杨梅果实成熟期正值梅雨季节,雨水过量会导致杨梅树大量落果,给果农造成损失.为此,市农科所开展了用防雨布保护杨梅果实的实验研究.在某杨梅果园随机选择40棵杨梅树,其中20棵加装防雨布(甲组),另外20棵不加装防雨布(乙组).在杨梅成熟期,统计了甲、乙两组中每一棵杨梅树的落果率(落地的杨梅颗数占树上原有杨梅颗数的百分比),绘制成统计图表(数据分组包含左端值不包含右端值).
甲组杨梅树落果率频数分布表
|
落果率 |
组中值 |
频数(棵 |
|
|
|
12 |
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
1 |
(1)甲、乙两组分别有几棵杨梅树的落果率低于 ?
(2)请用落果率的中位数或平均数,评价市农科所"用防雨布保护杨梅果实"的实际效果;
(3)若该果园的杨梅树全部加装这种防雨布,落果率可降低多少?说出你的推断依据.

如图,在四边形 中, , .
(1)求证: ;
(2)当 时,求 的度数.
