（本小题满分12分）下图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80~90分数段的学员数为21人
（Ⅰ）求该专业毕业总人数N和90~95分数段内的人数
；
（Ⅱ）现欲将90~95分数段内的名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为
，求名毕业生中男女各几人（男女人数均至少两人）？
（Ⅲ）在（Ⅱ）的结论下，设随机变量
表示n名毕业生中分配往乙学校的三名学生中男生的人数，求的分布列和数学期望．
一条直线经过点M（2，－3），倾斜角α=450，求这条直线方程.
已知数列
、
满足：
.
(1)求
；
(2) 证明数列
为等差数列，并求数列和的通项公式；
(3)设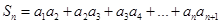
，求实数
为何值时
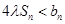恒成立。
已知不等式
的解集为
，
（1）求
的值；
（2）（文科做）解关于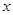
的不等式：
（2）（理科做）解关于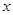的不等式：
．
运货卡车以每小时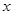
千米的速度匀速行驶130千米
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油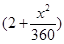
升，司机的工资是每小时14元.
（Ⅰ）求这次行车总费用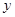
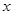关于的表达式；
（Ⅱ）当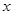为何值时，这次行车的总费用最低，并求出最低费用的值．
在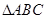
中，角
所对的边分别为
且满足
．
（1）求角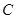
的大小；（2）求
的取值范围.