已知数列{
}中，
，且
对任意正整数都成立，数列{}的前n项和为Sn。
（1）若
，且
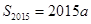，求a；
（2）是否存在实数k，使数列{}是公比不为1的等比数列，且任意相邻三项
按某顺序排列后成等差数列，若存在，求出所有k值，若不存在，请说明理由；
（3）若
。
【2015高考福建，理21】选修4-4：坐标系与参数方程
在平面直角坐标系
中，圆C的参数方程为
．在极坐标系（与平面直角坐标系取相同的长度单位，且以原点O为极点，以
轴非负半轴为极轴）中，直线l的方程为
（Ⅰ）求圆C的普通方程及直线l的直角坐标方程；
（Ⅱ）设圆心C到直线l的距离等于2，求m的值．
【2015高考福建，理21】选修4-2：矩阵与变换
已知矩阵
（Ⅰ）求A的逆矩阵
；
（Ⅱ）求矩阵C，使得AC=B．
D（选修4—5：不等式选讲）
解不等式
C（选修4—4：坐标系与参数方程）
已知圆C的极坐标方程为
，求圆C的半径．
B（选修4—2：矩阵与变换）
已知
，向量
是矩阵
的属性特征值
的一个特征向量，矩阵
以及它的另一个特征值．