、(满分14分)如图,正方体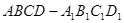 的棱长为2,E为AB的中点.
的棱长为2,E为AB的中点.
(Ⅰ)求证:
(Ⅱ)求异面直线BD1与AD所成角的余弦值。
(满分12分)某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19 .
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名?
(3)已知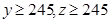 ,求初三年级中女生比男生多的概率。
,求初三年级中女生比男生多的概率。
(满分12分)现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,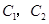 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组(1)求
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组(1)求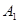 被选中的概率(2)求
被选中的概率(2)求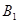 和
和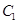 不全被选中的概率。
不全被选中的概率。
已知函数 ,若对任意
,若对任意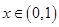 恒有
恒有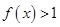 ,求
,求 的取值范围。
的取值范围。
.设函数f(x)=-a+x+a,x∈(0,1],a∈R*.
(1)若f(x)在(0,1]上是增函数,求a的取值范围;
(2)求f(x)在(0,1]上的最大值.