(本小题满分12分)在平面直角坐标系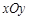 中,已知椭圆
中,已知椭圆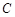 :
: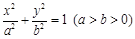 的离心率
的离心率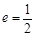 ,直线
,直线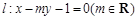 过椭圆
过椭圆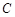 的右焦点
的右焦点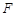 ,且交椭圆
,且交椭圆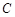 于
于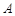 ,
,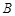 两点.
两点.
(1)求椭圆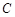 的标准方程;
的标准方程;
(2)已知点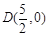 ,连结
,连结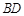 ,过点
,过点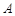 作垂直于
作垂直于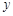 轴的直线
轴的直线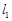 ,设直线
,设直线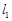 与直线
与直线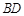 交于点
交于点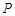 ,试探索当
,试探索当 变化时,是否存在一条定直线
变化时,是否存在一条定直线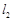 ,使得点
,使得点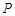 恒在直线
恒在直线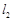 上?若存在,请求出直线
上?若存在,请求出直线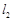 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)
设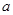 ∈R,函数
∈R,函数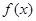 =
=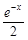 (
(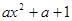 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <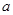 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
已知抛物线C:y2=2px(p>0)的焦点F和椭圆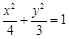 的右焦点重合,直线
的右焦点重合,直线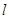 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点.
(1)求抛物线C的方程;
(2)若直线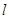 交y轴于点M,且
交y轴于点M,且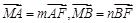 ,m、n是实数,对于直线
,m、n是实数,对于直线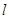 ,m+n是否为定值?若是,求出m+n的值,否则,说明理由.
,m+n是否为定值?若是,求出m+n的值,否则,说明理由.
为迎接建党90周年,某班开展了一次“党史知识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均为整数)进行统计,制成如图频率分布表:
(1)求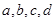 的值;
的值;
(2)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望.
如图所示,在矩形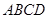 中,
中,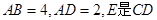 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且 .
.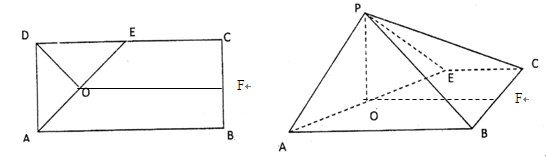
(1)求证:
(2)求二面角E-AP-B的余弦值.
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列 中的
中的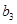 、
、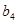 、
、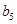 .
.
(1)求数列 的通项公式; (2)数列
的通项公式; (2)数列 的前n项和为
的前n项和为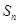 .
.