已知椭圆 的上顶点为
的上顶点为 ,直线
,直线 交椭圆于
交椭圆于 两点,设直线
两点,设直线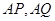 的斜率分别为
的斜率分别为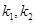 .
.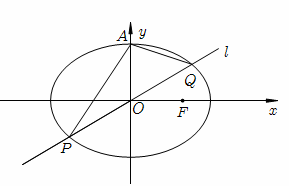
(1)若 时,求
时,求 的值;
的值;
(2)若 时,证明直线
时,证明直线 过定点.
过定点.
求函数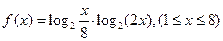 的最大值和最小值及相应的
的最大值和最小值及相应的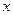 的值.
的值.
设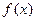 是定义在实数集
是定义在实数集 上的函数,且对任意实数
上的函数,且对任意实数 满足
满足 恒成立
恒成立
(1)求 ,
, ;
;
(2)求函数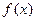 的解析式;
的解析式;
(3)若方程 恰有两个实数根在
恰有两个实数根在 内,求实数
内,求实数 的取值范围
的取值范围
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P(万元)和Q(万元),它们与投入资金x(万元)的关系,有经验公式: ,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?
,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?
已知函数
(1)判断函数 在
在 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)若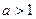 ,求
,求 在区间
在区间 上的最大值
上的最大值
已知如下两个命题: 函数
函数 的定义域为
的定义域为 ;
; 关于
关于 的方程
的方程 的两个实根
的两个实根 满足
满足 。
。
若命题“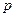 或
或 ”与命题“
”与命题“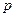 且
且 ”一真一假,求实数
”一真一假,求实数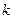 的取值范围
的取值范围