【原创】(本小题满分12分)在四棱锥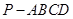 中,底面
中,底面 为菱形,
为菱形,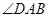 =
= ,平面
,平面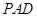 ⊥平面
⊥平面 ,
, =
= =
=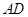 =2.
=2.
(Ⅰ)求证: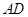 ⊥
⊥ ;
;
(Ⅱ)求三棱锥 的高.
的高.
某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
P(x)=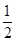 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
(1)写出第x月的需求量f(x)的表达式;
(2)若第x月的销售量g(x)=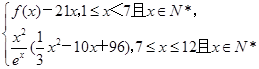
(单位:件),每件利润q(x)元与月份x的近似关系为:q(x)=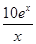 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
如图,在四棱锥PABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
设向量a=(2,sin θ),b=(1,cos θ),θ为锐角.
(1)若a·b=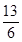 ,求sin θ+cos θ的值;
,求sin θ+cos θ的值;
(2)若a∥b,求sin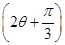 的值.
的值.
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|;
(3)设函数g(x)= ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
已知各项均为正数的数列{an}的前n项和为Sn,满足8Sn=a+4an+3(n∈N*),且a1,a2,a7依次是等比数列{bn}的前三项.
(1)求数列{an}及{bn}的通项公式;
(2)是否存在常数a>0且a≠1,使得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.