(本小题满分13分)如图,在矩形纸片ABCD中,AB=6,BC=12.将矩形纸片在右下角折起,使得该角的顶点落在矩形有左边上,设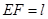 ,
,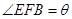 ,那么的长度取决于角
,那么的长度取决于角 的大小.
的大小.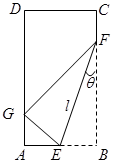
(1)写出用 表示
表示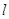 的函数关系式,并给出定义域;
的函数关系式,并给出定义域;
(2)求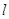 的最小值.
的最小值.
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如下茎叶图所示:
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2) 从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形,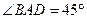 ,
, ,
, ,
, 是正三角形,平面
是正三角形,平面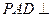 平面
平面 .
.
(1)求证: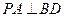 ;
;
(2)求三棱锥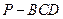 的体积.
的体积.
已知数列 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 的前
的前 项和为
项和为 .
.
(1)求通项 ;
;
(2)求 .
.
已知椭圆 ,
, 为坐标原点,椭圆的右准线与
为坐标原点,椭圆的右准线与 轴的交点是
轴的交点是 .
.
(1)点 在已知椭圆上,动点
在已知椭圆上,动点 满足
满足 ,求动点
,求动点 的轨迹方程;
的轨迹方程;
(2)过椭圆右焦点 的直线与椭圆交于点
的直线与椭圆交于点 ,求
,求 的面积的最大值
的面积的最大值
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:

(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均成绩.