如图,在四边形 中,
中,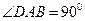 ,
,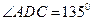 ,
, ,
, ,
,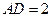 ,求四边形
,求四边形 绕
绕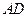 旋转一周所成几何体的表面积及体积.
旋转一周所成几何体的表面积及体积.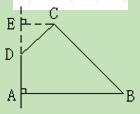
(本题满分10分)有20件产品,其中5件是次品,其余都是合格品,现不放回的从中依次抽2件.
求:⑴第一次抽到次品的概率;
⑵第一次和第二次都抽到次品的概率;
⑶在第二次抽到次品的概率.
(本题满分10分)已知在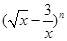 的展开式中,第4项为常数项
的展开式中,第4项为常数项
(1) 求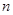 的值; (2) 求展开式中含
的值; (2) 求展开式中含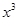 项系数.
项系数.
已知数列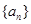 满足如图所示的程序框图。
满足如图所示的程序框图。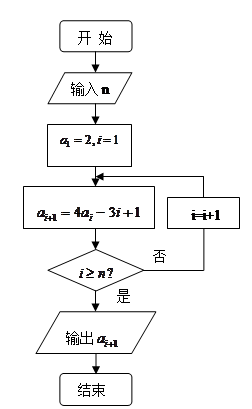
(I)写出数列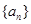 的一个递推关系式;并求数列
的一个递推关系式;并求数列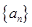 的通项公式
的通项公式
(Ⅱ)设数列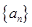 的前
的前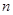 项和
项和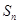 ,证明不等式
,证明不等式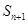 ≤
≤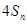 ,对任意
,对任意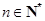 皆成立.
皆成立.
已知数列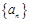 中,
中,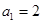 ,
, ,其前
,其前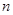 项和
项和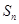
满足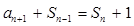
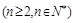 .
.
(Ⅰ)求证:数列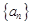 为等差数列,并求
为等差数列,并求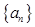 的通项公式;
的通项公式;
(Ⅱ)设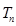 为数列
为数列 的前
的前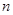 项和,求
项和,求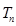
(Ⅲ)若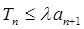 对一切
对一切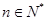 恒成立,求实数
恒成立,求实数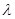 的最小值.
的最小值.
已知关于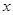 的不等式
的不等式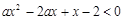
(1)当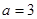 时,求此不等式解集;
时,求此不等式解集;
(2)当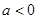 时,求此不等式解集。
时,求此不等式解集。