(本小题满分12分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人, 他们的健康状况如下表:
| 健康指数 |
2 |
1 |
0 |
-1 |
| 60岁至79岁的人数 |
120 |
133 |
34 |
13 |
| 80岁及以上的人数 |
9 |
18 |
14 |
9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
设函数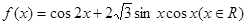 的最大值为
的最大值为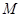 ,最小正周期为
,最小正周期为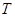 .
.
(Ⅰ)求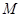 、
、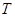 ;
;
(Ⅱ)若有10个互不相等的正数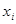 满足
满足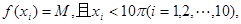 求
求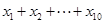 的值.
的值.
不等式选讲
已知 均为正实数,且
均为正实数,且 .求
.求 的最大值.
的最大值.
坐标系与参数方程
已知直线 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线 上求一点,使它到直线
上求一点,使它到直线 的距离最小,并求出该点坐标和最小距离.
的距离最小,并求出该点坐标和最小距离.
几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
已知函数 (
( ),其中
),其中 .
.
(1)当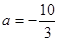 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(3)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.