甲、乙两人参加某种选拔测试.在备选的 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是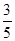 ,乙能答对其中的
,乙能答对其中的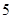 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的 道题中随机抽出
道题中随机抽出 道题进行测试,答对一题加
道题进行测试,答对一题加 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减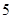 分,至少得
分,至少得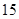 分才能入选.
分才能入选.
(Ⅰ)求乙的得分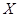 的分布列和数学期望
的分布列和数学期望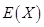 ;
;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?(用线性规划求解要画出规范的图形)
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用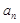 的信息如下图。
的信息如下图。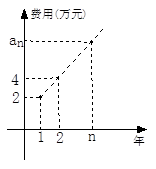
(1)求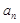 ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
已知p: , q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
, q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
(1)若不等式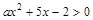 的解集是
的解集是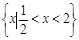 ,求不等式
,求不等式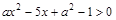 的解集.
的解集.
(2) ,试比较
,试比较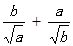 与
与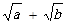 的大小。
的大小。
设函数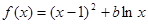 ,其中
,其中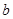 为常数.
为常数.
(1)当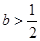 时,判断函数
时,判断函数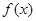 在定义域上的单调性;
在定义域上的单调性;
(2)若函数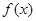 有极值点,求
有极值点,求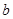 的取值范围及
的取值范围及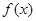 的极值点.
的极值点.