如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路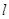 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数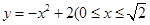 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为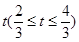 .
.
(1)当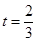 时,求直路
时,求直路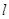 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路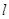 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?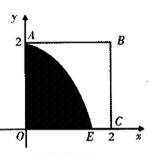
对于数列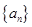 :
:
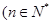 ,实常数
,实常数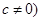
(1)求 ,并猜想
,并猜想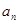 (2)证明你的猜想.
(2)证明你的猜想.
已知函数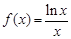 .
.
(1)求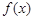 在点
在点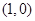 处的切线方程;
处的切线方程;
(2)求函数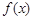 在
在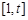 上的最大值.
上的最大值.
设实数数列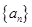 的前
的前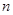 项和
项和 ,满足
,满足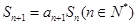
(1)若 成等比数列,求
成等比数列,求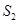 和
和 ;
;
(2)求证:当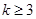 时,
时,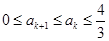 .
.
过曲线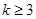 :
: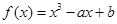 外的点
外的点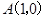 作曲线
作曲线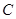 的切线恰有两条,
的切线恰有两条,
(1)求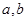 满足的等量关系;
满足的等量关系;
(2)若存在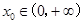 ,使
,使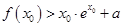 成立,求
成立,求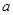 的取值范围.
的取值范围.
包含甲在内的甲、乙、丙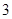 个人练习传球,设传球
个人练习传球,设传球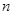 次,每人每次只能传一下,首先从甲手中传出,第
次,每人每次只能传一下,首先从甲手中传出,第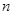 次仍传给甲,共有多少种不同的方法?
次仍传给甲,共有多少种不同的方法?
为了解决上述问题,设传球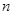 次,第
次,第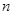 次仍传给甲的传球方法种数为
次仍传给甲的传球方法种数为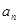 ;设传球
;设传球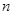 次,第
次,第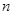 次不传给甲的传球方法种数为
次不传给甲的传球方法种数为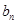 .根据以上假设回答下列问题:
.根据以上假设回答下列问题:
(1)求出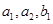 的值;
的值;
(2)根据你的理解写出 与
与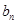 的关系式;
的关系式;
(3)求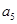 的值及通项公式
的值及通项公式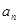 .
.