设函数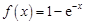 .
.
(Ⅰ)证明:当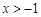 时,
时,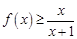 ;
;
(Ⅱ)设当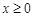 时,
时,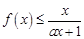 ,求实数
,求实数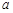 的取值范围.
的取值范围.
已知数列 的前n项和Sn=9-6n.
的前n项和Sn=9-6n.
(1)求数列 的通项公式.
的通项公式.
(2)设 ,求数列
,求数列 的前n项和.
的前n项和.
已知定义域为R的函数 满足
满足
(I)若 ,求
,求 ;又若
;又若 ,求
,求 ;
;
(II)设有且仅有一个实数 ,使得
,使得 ,求函数
,求函数 的解析表达式
的解析表达式
已知a>0,函数f(x)=ax-bx2,
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明:a≤2 ;
;
(2)当b>1时,证明:对任意x∈[0, 1], |f(x)|≤1的充要条件是:b-1≤a≤2 ;
;
(3)当0<b≤1时,讨论:对任意x∈[0, 1], |f(x)|≤1的充要条件。
设集合 ,
, .若
.若 ,求实数
,求实数 的取值范围.
的取值范围.
在 轴同侧的两个圆:动圆
轴同侧的两个圆:动圆 和圆
和圆 外切(
外切( ),且动圆
),且动圆 与
与 轴相切,求
轴相切,求
(1)动圆 的圆心轨迹方程L;
的圆心轨迹方程L;
(2)若直线 与曲线L有且仅有一个公共点,求
与曲线L有且仅有一个公共点,求 之值。
之值。