为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: .
.
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的
岁的
人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场
的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要
负责人,记这3名志愿者中“年龄低于35岁”的人数为 ,求
,求 的分布列及
的分布列及
数学期望.
已知函数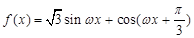

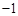
( ),且函数
),且函数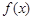 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求函数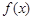 的解析式;
的解析式;
(Ⅱ)在△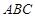 中,角
中,角 所对的边分别为
所对的边分别为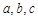 .若
.若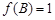 ,
,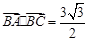 ,且
,且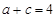 ,试求
,试求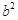 的值.
的值.
已知 ,直线l:
,直线l: ,椭圆C:
,椭圆C: ,
, ,
, 分别为椭圆C的左、右焦点。
分别为椭圆C的左、右焦点。
(Ⅰ)当直线l过右焦点 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点。
(ⅰ)求线段AB长度的最大值;
(ⅱ) ,
, 的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数
的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数 的取值范围。
的取值范围。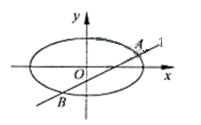
已知曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差是1。
(Ⅰ)求曲线C的方程;
(Ⅱ)过点K(-1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D。证明:点F在直线BD上;
过点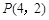 作直线l交x轴于A点、交y轴于B点,且P位于AB两点之间。
作直线l交x轴于A点、交y轴于B点,且P位于AB两点之间。
(Ⅰ) ,求直线l的方程;
,求直线l的方程;
(Ⅱ)求当 取得最小值时直线l的方程。
取得最小值时直线l的方程。
已知双曲线C关于两条坐标轴都对称,且过点 ,直线
,直线 与
与 (
( ,
, 为双曲线C的两个顶点)的斜率之积
为双曲线C的两个顶点)的斜率之积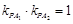 ,求双曲线C的标准方程。
,求双曲线C的标准方程。