（本小题满分12分）已知数列{an}，{bn}满足：a1b1＋a2b2＋a3b3＋…＋anbn＝
（
）.
（Ⅰ）若{bn }是首项为1，公比为2等比数列，求数列{an}的通项公式；
（Ⅱ）在数列{an}中，a1＝1，对任意
，
，记数列{an＋bn}的前n项和为Tn，求满足不等式
的自然数n的最小值．
（本小题10分）
已知两点A（0,1），B（2,m）， 如果经过A与B且与x轴相切的圆有且只有一个，求m的值及圆的方程。
（本题12分）已知函数
，
（1）若
，求
的单调区间；
（2）若
恒成立，求
的取值范围。
（本题12分）已知：数列
的前n项和为
，满足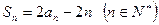
（1）求数列的通项公式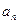
（2）若数列
满足
，
为数列
的前n项和，求证：
（3）数列中是否存在三项
，
，
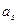成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由。
（本题12分）已知：函数
（1）当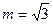
时，求函数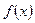
的单调递增区间；
（2）设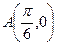
，
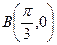，存在函数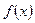图像的一个对称中心落在线段AB上，求m的取值范围。
（本题12分）已知：两点
，
，且点P使
，
，
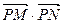成公差小于零的等差数列
（1）点P的轨迹是什么曲线？
（2）若点P坐标为
，
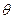为
，
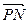的夹角，求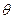的取值范围。