（本题12分）已知：数列
的前n项和为
，满足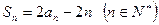
（1）求数列的通项公式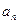
（2）若数列
满足
，
为数列
的前n项和，求证：
（3）数列中是否存在三项
，
，
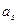成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由。
（本小题满分12分）设函数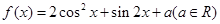
．
（1）求函数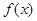
的最小正周期和单调递增区间；
（2）当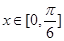
时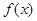，的最大值为2，求
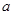的值，并求出
的对称轴方程．
（本小题满分12分）学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数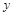
与听课时间
（单位：分钟）之间的关系满足如图所示的图象，当
时，图象是二次函数图象的一部分，其中顶点A（10，80），过点B（12，78）；当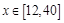
时，图象是线段BC，其中C（40，50）.根据专家研究，当注意力指数大于62时，学习效果最佳。
（1）试求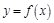
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由。
（本小题满分13分）如图，以Ox为始边作角α与β（
） ，它们终边分别单位圆相交于点P、Q，已知点P的坐标为（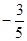
，
）.
（1）求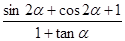
的值；
（2）若
·
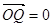，求
.
（本小题满分12分） 已知集合
，集合
．
（1）当
时，求
；
（2）若
,求实数
的取值范围;
（3）若
,求实数的取值范围．
（本小题满分14分）已知数列
中
.
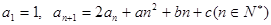为实常数．
（Ⅰ）若
，求数列的通项公式；
（Ⅱ）若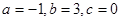
.
①是否存在常数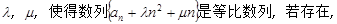
求出
的值，若不存在，请说明理由；
②设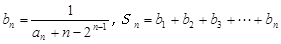 
.证明：n≥2时，
.