(本小题满分12分)学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数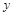 与听课时间
与听课时间 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当
时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当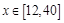 时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳。
时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳。
(1)试求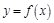 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由。
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
10 |
||
| 乙班 |
30 |
||
| 合计 |
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
(本小题共12分)已知函数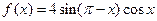
(Ⅰ)求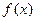 的最小正周期; (Ⅱ)若
的最小正周期; (Ⅱ)若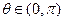 ,
,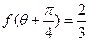 , 求
, 求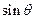 的值
的值
(本小题共13分)
已知 ,
, 或1,
或1,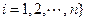
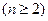 ,对于
,对于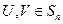 ,
, 表示U和V中相对应的元素不同的个数.
表示U和V中相对应的元素不同的个数.
(Ⅰ)令 ,存在m个
,存在m个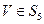 ,使得
,使得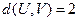 ,写出m的值;
,写出m的值;
(Ⅱ)令 ,若
,若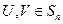 ,求证:
,求证: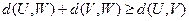 ;
;
(Ⅲ)令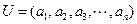 ,若
,若 ,求所有
,求所有 之和.
之和.
(本小题共14分)
已知点 ,
,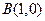 ,
, 动点P满足
动点P满足 ,记动点P的轨迹为W.
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线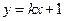 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点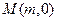 ,使得
,使得 成立,求实数m的取值范围.
成立,求实数m的取值范围.
(本小题共13分)
已知函数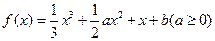 ,
, 为函数
为函数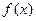 的导函数.
的导函数.
(Ⅰ)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是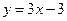 ,求
,求 的值;
的值;
(Ⅱ)若函数 ,求函数
,求函数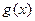 的单调区间.
的单调区间.