(本小题共12分)已知函数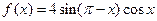
(Ⅰ)求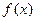 的最小正周期; (Ⅱ)若
的最小正周期; (Ⅱ)若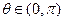 ,
,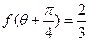 , 求
, 求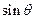 的值
的值
(本小题满分12分)
如图,在平行四边形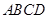 中,
中,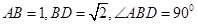 ,将它们沿对角线
,将它们沿对角线 折起,折后的点
折起,折后的点 变为
变为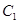 ,且
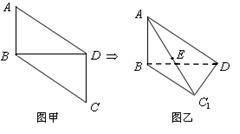
,且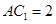 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)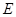 为线段
为线段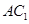 上的一个动点,当线段
上的一个动点,当线段 的长为多少时,
的长为多少时,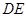 与平面
与平面 所成的角为
所成的角为 ?
?
(本小题满分12分)
已知双曲线C与椭圆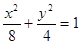 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为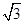 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)若直线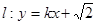 与双曲线
与双曲线 有两个不同的交点
有两个不同的交点 和
和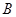 ,且
,且
(其中 为原点),求
为原点),求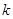 的取值范围.
的取值范围.
(本小题满分10分)
已知抛物线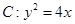 与直线
与直线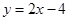 交于
交于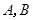 两点.
两点.
(Ⅰ)求弦 的长度;
的长度;
(Ⅱ)若点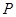 在抛物线
在抛物线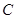 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标.
(本小题满分12分)
在如图的多面体中,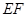 ⊥平面
⊥平面 ,
,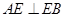 ,
,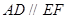 ,
,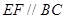 ,
,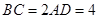 ,
,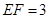 ,
,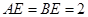 ,
, 是
是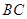 的中点.
的中点.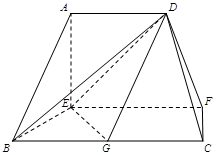
(Ⅰ) 求证: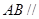 平面
平面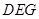 ;
;
(Ⅱ) 求二面角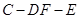 的余弦值.
的余弦值.
如图,设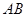 、
、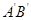 分别是圆
分别是圆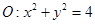 和椭圆
和椭圆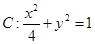 的弦,且弦的端点在
的弦,且弦的端点在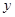 轴的异侧,端点
轴的异侧,端点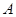 与
与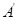 、
、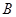 与
与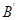 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
(Ⅰ)若弦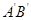 所在直线斜率为
所在直线斜率为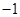 ,且弦
,且弦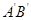 的中点的横坐标为
的中点的横坐标为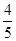 ,求直线
,求直线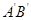 的方程;
的方程;
(Ⅱ)若弦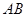 过定点
过定点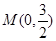 ,试探究弦
,试探究弦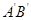 是否也必过某个定点. 若有,请证明;若没有,请说明理由.
是否也必过某个定点. 若有,请证明;若没有,请说明理由.