(本小题满分13分)如图,以Ox为始边作角α与β( ) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为(
) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为(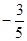 ,
, ).
).
(1)求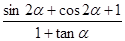 的值;
的值;
(2)若 ·
·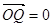 ,求
,求 .
.
我们已经学过了等比数列,你是否想过有没有等积数列呢?
(1)类比“等比数列”给出“等积数列”的定义;
(2)探索每一项都不为0等积数列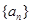 的奇数项与偶数项各有什么特点。
的奇数项与偶数项各有什么特点。
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点。
的焦点。
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若 的值。
的值。
已知函数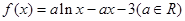
(1)当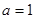 时,求函数
时,求函数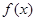 的单调区间;
的单调区间;
(2)若函数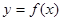 的图像在点
的图像在点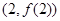 处的切线的倾斜角为
处的切线的倾斜角为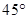 ,问:
,问: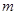 在什么范围取值时,函数
在什么范围取值时,函数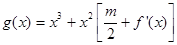 在区间
在区间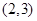 上总存在极值?
上总存在极值?
一个多面体的直观图和三视图如下: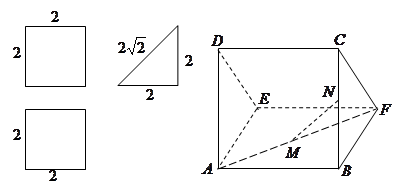
(其中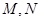 分别是
分别是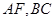 中点)
中点)
(1)求证: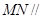 平面
平面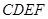 ;
;
(2)求多面体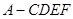 的体积.
的体积.
f(x)=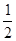 x2+
x2+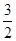 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令bn=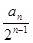 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn