有人设想:可以在飞船从运行轨道进入返回地球程序时，借飞船需要减速的机会，发射一个小型太空探测器，从而达到节能的目的。如图所示，飞船在圆轨道Ⅰ上绕地球飞行，其轨道半径为地球半径的k倍（k>1）。当飞船通过轨道Ⅰ的A点时，飞船上的发射装置短暂工作，将探测器沿飞船原运动方向射出，并使探测器恰能完全脱离地球的引力范围，即到达距地球无限远时的速度恰好为零，而飞船在发射探测器后沿椭圆轨道Ⅱ向前运动，其近地点B到地心的距离近似为地球半径R。以上过程中飞船和探测器的质量均可视为不变。已知地球表面的重力加速度为g。
（1）求飞船在轨道Ⅰ运动的速度大小；
（2）若规定两质点相距无限远时引力势能为零，则质量分别为M、m的两个质点相距为r时的引力势能
，式中G为引力常量。在飞船沿轨道Ⅰ和轨道Ⅱ的运动过程，其动能和引力势能之和保持不变；探测器被射出后的运动过程中，其动能和引力势能之和也保持不变。
①求探测器刚离开飞船时的速度大小；
②已知飞船沿轨道Ⅱ运动过程中，通过A点与B点的速度大小与这两点到地心的距离成反比。根据计算结果说明为实现上述飞船和探测器的运动过程，飞船与探测器的质量之比应满足什么条件。
飞机着陆后做匀变速直线运动，速度逐渐减小，已知飞机着陆时的速度为60m/s，若前5s内通过的位移为225m，则飞机的加速度大小为多少？此后飞机还要滑行多长时间才能停止运动？
某人在离地10m阳台用10m/s的速度竖直上抛一个质量为1kg的柚子（不计空气阻力），试问：
（1）此人对柚子做的功；
（2）在离地什么高度时柚子的动能等于重力势能二分之一．
在一次军事演习中，解放军战士为了让炮弹以200m/s的速度击中前方450m高山崖上的某处军事目标，那大炮射击时至少需要让炮弹以多少的速度射出？
一位质量m=50kg的滑雪运动员从高度h=30m的斜坡自由滑下（初速度为零）。斜坡的倾角θ=37°，滑雪板与雪面滑动摩擦因素
=0.1。则运动员滑至坡底的过程中有：
（1）所受几个力所做的功各是多少？
（2）合力做了多少功？
（3）到达坡底时摩擦力的功率是多少？（不计空气阻力）
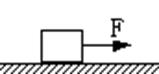
如图，一质量为5kg的滑块在F=15N的水平拉力作用下，由静止开始做匀加速直线运动，若滑块与水平地面间的动摩擦因数为0.2，g取10m/s2,问：滑块运动的加速度多大？滑块在力F作用下经5s通过的位移是多大？