如图所示,空间存在竖直向上的匀强磁场,磁感应强度B=0.50T,两条光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.40m,左端接有阻值R=0.40Ω的电阻。一质量m=0.10kg、阻值r=0.10Ω的金属棒MN放置在导轨上。金属棒在水平向右的拉力F作用下,沿导轨做速度v=2.0m/s的匀速直线运动。求: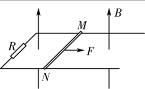
(1)通过电阻R的电流I;
(2)拉力F的大小;
(3)撤去拉力F后,电阻R上产生的焦耳热Q。
一半径为 的 球体放置在水平面上,球体由折射率为 的透明材料制成。现有一束位于过球心 的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示。已知入射光线与桌面的距离为 。求出射角。
1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为
,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为
的匀强磁场与盒面垂直。
处粒子源产生的粒子,质量为
、电荷量为
,在加速器中被加速,加速电压为
。加速过程中不考虑相对论效应和重力作用。
(1) 求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2) 求粒子从静止开始加速到出口处所需的时间 ;
(3) 实际使用中,磁感应强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为 、 ,试讨论粒子能获得的最大动能 。
"探究加速度与物体质量、物体受力的关系"的实验装置如图甲所示.
(1)在平衡小车与桌面之间摩擦力的过程中,打出了一条纸袋如图乙所示。计时器打点的时间间隔为0.02
.从比较清晰的点起,每5个点取一个计数点,量出相邻计数点之间的距离。该小车的加速度
=
.(结果保留两位有效数字)

(2)平衡摩擦力后,将5个相同的砝码都放在小车上.挂上砝码盘,然后每次从小车上取一个砝码添加到砝码盘中,测量小车的加速度。小车的加速度
与砝码盘中砝码总重力F的实验数据如下表
| 砝码盘中砝码总重力
(
) |
0.196 |
0.392 |
0.588 |
0.784 |
0.980 |
| 加速度
(
) |
0.69 |
1.18 |
1.66 |
2.18 |
2.70 |
请根据实验数据作出
的关系图像
(3)根据提供的试验数据作出的 图线不通过原点,请说明主要原因。
一气象探测气球,在充有压强为
(即
)、温度为
的氦气时,体积为
。在上升至海拔
高空的过程中,气球内氦气逐渐减小到此高度上的大气压
,气球内部因启动一持续加热过程而维持其温度不变。此后停止加热,保持高度不变。已知在这一海拔高度气温为
。求:
(1)氦气在停止加热前的体积;
(2)氦气在停止加热较长一段时间后的体积。
如图,
是边长为
的正方形。质量为
、电荷量为
的电子以大小为
的初速度沿纸面垂直于
边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从
边上的任意点入射,都只能从
点射出磁场。不计重力,求:
(1)次匀强磁场区域中磁感应强度的方向和大小;
(2)此匀强磁场区域的最小面积。