变化的磁场可以激发感生电场,电子感应加速器就是利用感生电场使电子加速的设备。它的基本原理如图所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空室内做圆周运动。电磁铁线圈电流的大小、方向可以变化,在两极间产生一个由中心向外逐渐减弱、而且变化的磁场,这个变化的磁场又在真空室内激发感生电场,其电场线是在同一平面内的一系列同心圆,产生的感生电场使电子加速。图1中上部分为侧视图、下部分为俯视图。已知电子质量为m、电荷量为e,初速度为零,电子圆形轨道的半径为R。穿过电子圆形轨道面积的磁通量Φ随时间t的变化关系如图2所示,在t0时刻后,电子轨道处的磁感应强度为B0,电子加速过程中忽略相对论效应。
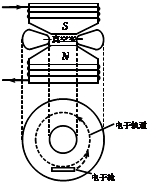
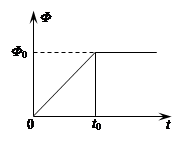
|
(1)求在t0时刻后,电子运动的速度大小;
(2)求电子在整个加速过程中运动的圈数; 。请进一步说明在电子加速过程中,某一确定时刻电子轨道处的磁感应强度与电子轨道内的平均磁感应强度的关系。
。请进一步说明在电子加速过程中,某一确定时刻电子轨道处的磁感应强度与电子轨道内的平均磁感应强度的关系。如图甲所示,竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成,AB和BCD相切于B点,CD连线是圆轨道竖直方向的直径(C、D为圆轨道的最低点和最高点),已知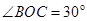 。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取
。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取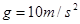 。求:
。求: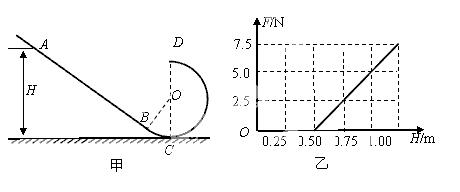
(1)滑块的质量和圆轨道的半径;
(2)是否存在某个H值,使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点。若存在,请求出H值;若不存在,请说明理由。
如图所示,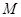 是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴
是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴 匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为
匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为 .已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求:
.已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求:
(1)每一滴水经多长时间滴落到盘面上?
(2)要使每一滴水在盘面上的落点都位于同一直线上,圆盘转动的角速度ω应为多大?
(3)第二滴水与第三滴水在盘面上落点间的最大距离x.
一个滑雪的人,由静止从山坡上匀变速滑下,山坡的总长为25m, 当他经过5秒时刚好到达山坡中点。求
(1)他在山坡上的加速度大小
(2)他到达坡底的速度的大小
(3)他从山坡上滑下的总时间
一物体向北做匀变速直线运动,经0.2 s时间速度由12 m/s减少到8 m/s,求:该物体的加速度大小为多少m/s2?加速度的方向?
如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C,一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板,滑板运动到C时被牢固粘连,物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长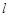 =6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g。
=6.5R,板右端到C的距离L在R<L<5R范围内取值,E距A为S=5R,物块与传送带、物块与滑板间的动摩擦因数均μ=0.5,重力加速度取g。
(1)求物块滑到B点的速度大小;
(2)试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功Wf与L的关系,并判断物块能否滑到CD轨道的中点。