如图,已知抛物线 与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线
与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线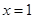 .
.
(1)求抛物线的解析式;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.
如图, 是半径为
是半径为 的
的 上的定点,动点
上的定点,动点 从
从 出发,以
出发,以 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点 回到
回到 地立即停止运动.
地立即停止运动.
(1)如果 ,求点
,求点 运动的时间;
运动的时间;
(2)如果点 是
是 延长线上的一点,
延长线上的一点, ,那么当点
,那么当点 运动的时间为
运动的时间为 时,判断直线
时,判断直线 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20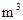 时,按2元/
时,按2元/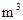 计费;月用水量超过20
计费;月用水量超过20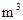 时,其中的20
时,其中的20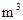 仍按2元/
仍按2元/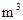 收费,超过部分按
收费,超过部分按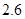 元/
元/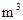 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费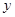 元.
元.
(1)分别求出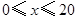 和
和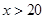 时
时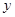 与
与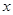 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 |
四月份 |
五月份 |
六月份 |
| 交费金额 |
30元 |
34元 |
42.6元 |
小明家这个季度共用水多少立方米?
如图,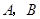 两地之间有一座山,汽车原来从
两地之间有一座山,汽车原来从 地到
地到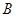 地须经
地须经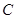 地沿折线
地沿折线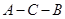 行驶,现开通隧道后,汽车直接沿直线
行驶,现开通隧道后,汽车直接沿直线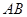 行驶.已知
行驶.已知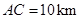 ,
,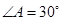 ,
,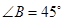 ,则隧道开通后,汽车从
,则隧道开通后,汽车从 地到
地到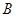 地比原来少走多少千米?(结果精确到
地比原来少走多少千米?(结果精确到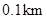 )(参考数据:
)(参考数据: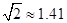 ,
,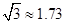 )
)
将 四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
(1) 在甲组的概率是多少?
在甲组的概率是多少?
(2)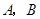 都在甲组的概率是多少?
都在甲组的概率是多少?
两组邻边分别相等的四边形我们称它为菱形.
如图,在菱形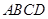 中,
中,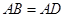 ,
,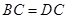 ,
,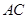 ,
,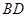 相交于点
相交于点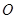 ,
,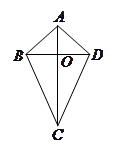
(1)求证:①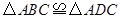 ;
;
②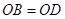 ,
,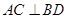 ;
;
(2)如果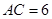 ,
,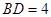 ,求菱形
,求菱形 的面积.
的面积.