班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如图1的频数分布折线图.
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有____人、女生有____人;
②男、女生发言次数的中位数分别是____ 次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.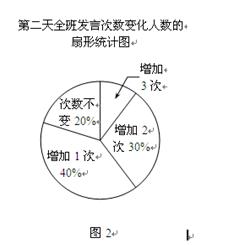
如图,在平面直角坐标系中放置一直角三角板,其顶点为 ,
, ,
, ,将此三角板绕原点
,将此三角板绕原点 顺时针旋转
顺时针旋转 ,得到
,得到 .
.
(1)如图,一抛物线经过点 ,求该抛物线解析式;
,求该抛物线解析式;
(2)设点 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点
的面积达到最大时点 的坐标及面积的最大值.
的坐标及面积的最大值.
如图,在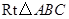 中,斜边
中,斜边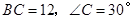 ,
, 为
为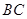 的中点,
的中点,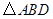 的外接圆
的外接圆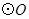 与
与 交于
交于 点,过
点,过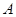 作
作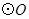 的切线
的切线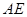 交
交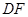 的延长线于
的延长线于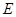 点.
点.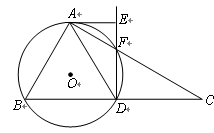
(1)求证: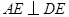 ;
;
(2)计算: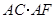 的值.
的值.
“六一”儿童节,小明与小亮受邀到科技馆担任义务讲解员,他们俩各自独立从A区(时代辉煌)、B区(科学启迪)、C区(智慧之光)、D区(儿童世界)这四个主题展区中随机选择一个为参观者服务.
(1)请用列表法或画树状图法说明当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况.(用字母表示)
(2)求小明与小亮只单独出现在B区(科学启迪)、C区(智慧之光)、D区(儿童世界)三个主题展区中担任义务讲解员的概率.
如图,在梯形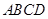 中,
中,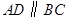 ,
,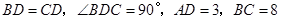 .求
.求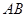 的长.
的长.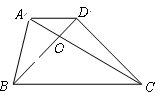
某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.