如图， AD平分∠EAC．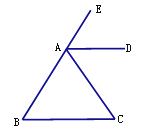
（1）若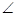
B＝50°AD∥BC，
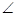则DAC＝ °；
（2）若∠C=55°，∠EAC=110°，AD与BC平行吗？
为什么？
根据解答过程填空（填理由或数学式）．
解：∵AD平分∠EAC（已知）
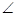∴DAC＝
（ ）°（角平分线的定义）
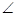∵C＝55°（已知）
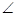∴C＝（ ） （ ）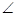
∴AD∥BC（ ）
（·湖北鄂州，24题，12分）如图，在平面直角坐标系xoy中，直线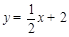
与x 轴交于点A，与y轴交于点C．抛物线y=ax2+bx+c的对称轴是
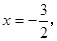且经过A、C两点，与x轴的另一交点为点B．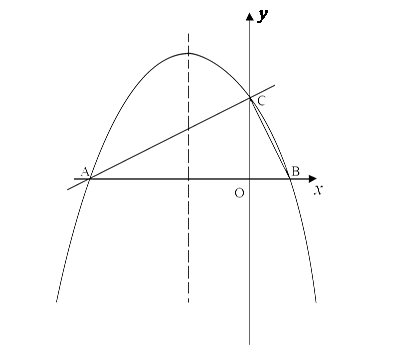
（1）①直接写出点B的坐标；②求抛物线解析式．
（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标．
（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
（·湖北衡阳，28题，分）（本小题满分10分）
如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连结CP，过点P作PM⊥CP交AB于点D，且PM＝CP，过点M作MN∥OA，交BO于点N，连结ND、BM，设OP＝
．
（1）求点M的坐标（用含的代数式表示）；
（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由；
（3）当为何值时，四边形BNDM的面积最小．
（·湖南株洲）为了举行班级晚会，孔明准备去商店购买20乒乓球做道具，并买一些乒乓球拍做奖品，已知乒乓球每个1．5元，球拍每个22元，如果购买金额不超过200元，且买的球拍尽可能多，那么孔明应该买多少个球拍？
（·湖南益阳）大学生小刘回乡创办小微企业，初期购得原材料若干吨，每天生产相同件数的某种产品，单件产品所耗费的原材料相同．当生产6天后剩余原材料36吨，当生产10天后剩余原材料30吨．若剩余原材料数量小于或等于3吨，则需补充原材料以保证正常生产．
（1）求初期购得的原材料吨数与每天所耗费的原材料吨数；
（2）若生产16天后，根据市场需求每天产量提高20%，则最多再生产多少天后必须补充原材料？
（·湖南长沙）现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12．1万件。现假定该公司每月的投递总件数的增长率相同：
（1）求该快递公司投递快递总件数的月平均增长率；
（2）如果平均每人每月最多可投递快递0．6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？