一台汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求汽车原来的速度.
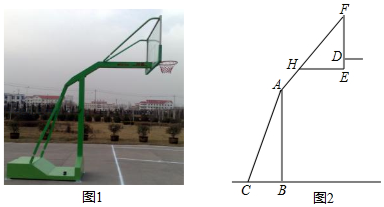
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,
收发微信红包已成为各类人群进行交流联系、增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?

如图,已知 是 的直径, 与 相切于 , .
(1)求证: 是 的平分线;
(2)若 , 的半径 ,求 的长.

如图,已知反比例函数 的图象经过点 , 轴,且 的面积为2.
(1)求 和 的值;
(2)若点 也在反比例函数 的图象上,当 时,求函数值 的取值范围.

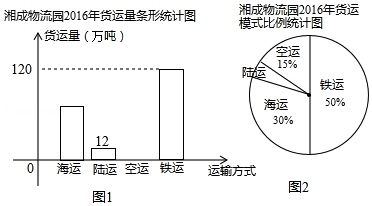
在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数.